Photoacoustic tomography (PAT) is a noninvasive imaging modality which exploits the differential absorption of light by biomolecules to allow noninvasive visualization of soft tissues in living organisms, specifically for early diagnosis of cancer. The focus of my Ph.D. research has been the development of novel reconstruction approaches for PAT, which aim to capture optical contrast within an object from photoacoustically generated ultrasound amplitudes measured at the boundary. Since ultrasound propagation is relatively scatter-free, the absorption coefficient images from PAT are of better spatial resolution. The inverse problem is ill-posed because of data which is both noisy and sparse. Moreover, since the optical contrast is traditionally recovered from the absorbed energy reconstructed from boundary pressure data through a second iteration, the algorithm is computation-intensive. Development of fast and reliable algorithms have been attempted, some of which try to recover the unknown absorption coefficient directly, and others through a noniterative procedure from the recovered absorbed energy density.

Noniterative inversion strategy for quantitative PAT

The first development is a robust deterministic algorithm wherein the absorption coefficient is recovered noniteratively from the reconstructed absorbed energy by first solving for fluence from the photon propagation equation and dividing the absorbed energy with it. The absorbed energy is recovered from the boundary pressure either iteratively using the wave equation with the second-order absorbing boundary condition as the forward model or a simpler generalized backprojection algorithm. Using the cross-section of a cylinder of 30 mm radius as the computational domain, we discretize the elliptic partial differential equation using linear triangular finite element method (FEM) to solve the forward problem. Synthetic experimental data, wherever needed, is generated by adding 1-5% Gaussian noise to these frequency components of boundary pressure. Since the diffusion approximation to the radiative transfer equation (RTE) holds good only at distances greater than one transport mean-free path inside the medium, Monte Carlo (MC) simulations have also been used to compute the fluence distribution and subsequently generate boundary pressure data. In figure 1(b), we show the absorption coefficient distribution reconstructed using the proposed noniterative algorithm for a single light source and observe that it compares well with the reference in figure 1(a). We also show in figures 1(c) and 1(d) that the absorbed energy recovery using three sources for uniform illumination yields a closer approximation to the reference optical contrast than that obtained using a single source. In our work, we also demonstrate that the inclusions near the boundary can be more accurately reconstructed using fluence recovered through MC simulations where the diffusion equation (DE) fails to hold.
The noniterative algorithm developed for quantitative photoacoustic tomography is also validated on absorbed energy maps obtained from experimental pressure data through filtered backprojection. As seen in figure 2(a), the recovered absorbed energy map as such appears edge-enhanced for the inclusions, which could be due to the non-uniform fluence distribution and the fact that the data was acquired only at considerably higher frequencies. To correct for this, particularly the non-uniform fluence, we input this energy distribution into the DE as discussed earlier to recover fluence and subsequently obtain the absorption coefficient through division. This procedure maybe repeated to obtain a corrected fluence distribution and a closer approximation of the optical contrast as shown in figure 2(b).

Figure 1. (a) Reference absorption coefficient distribution

Figure 1. (b) Recovered absorption coefficient using DE as the forward model for light propagation with a single light source

Figure 1. (c) Reconstructed absorbed energy for a single source using the diffusion equation to compute fluence

Figure 2. (a) Absorbed energy map obtained through backprojection

Figure 1. (d) Reconstructed absorbed energy for three sources using MC simulation to compute fluence

Figure 2. (b) Recovered absorption coefficient through noniterative quantitative photoacoustic tomography

Adaptive extended Kalman filter for accelerated shape based reconstruction

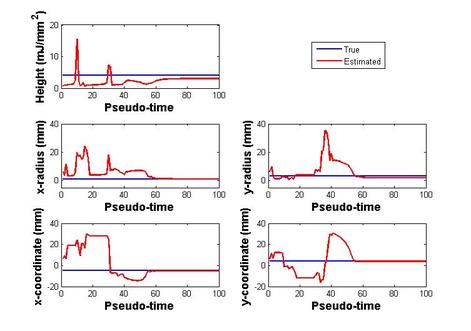
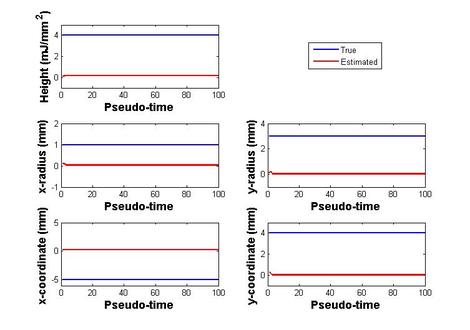
The rest of the algorithms developed use a pseudo-dynamic stochastic filtering approach wherein the process equation is set up such that its steady-state solution, guided by the measured pressure, gives the desired parameter values. Towards this, an extended Kalman filter (EKF) is set up for arriving at  inhomogeneities, which is the second algorithm developed. To keep the dimension of the source recovery problem within limits that can be handled by the EKF, the absorbed energy of the inclusions are represented using simple geometrical shapes such as Gaussian distributions. This facilitates an accelerated tracking of inclusion locations using data at a single frequency in contrast to the previously developed Gauss-Newton (GN) reconstruction using multiple frequencies. Consequently, it bypasses the error-prone construction of Jacobian for multiple frequencies saving on computation time. This strategy also eases the constraint on using finely refined meshes while solving the forward problem at higher wave numbers by employing a relatively lower frequency for reconstruction. In figure 3(b), we show the recovered elliptical approximation to the irregularly shaped inhomogeneity shown in figure 3(a). Figure 3(c) depicts the estimation trajectories for the individual parameters and the closeness with the true values. However, the use of EKF is confounded by the requirement of correct selection (tuning) of error and process covariances. Figure 3(d) shows the effect of improper tuning of error covariances. To address this difficulty, we show the implementation of adaptive approaches for tuning and compare them with manually-tuned filters for varying noise levels.

Figure 3. (a) Reference absorbed energy distribution

Figure 3. (b) Recovered absorbed energy using EKF estimates

Figure 3. (c) Trajectories of estimates for Gaussian distribution parameters

Figure 3. (d) Estimation trajectories when the filter is not properly tuned

Two-stage reconstruction using Newton-directed ensemble Kalman filter

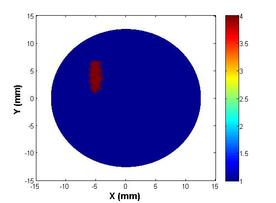
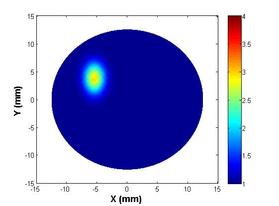
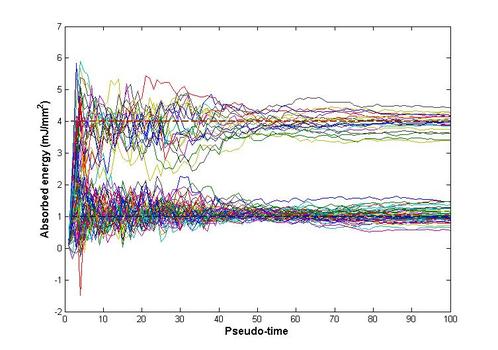
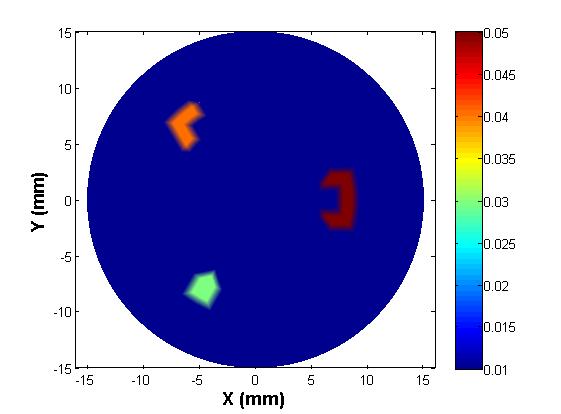
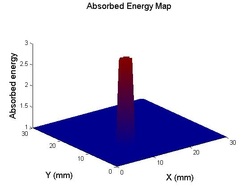
The third approach, the pseudo-dynamic ensemble Kalman filter (PD-EnKF), is developed to circumvent two major shortcomings of the EKF, namely filter divergence in the absence of proper tuning and inability to handle larger sets of unknowns. Even though the PD-EnKF uses a Kalman-gain based parameter update, it computes error covariance updates using Monte Carlo simulations. The inclusion locations are first expediently predicted with a shape-based PD-EnKF using data at a single frequency and then the shape and parameter variations within are arrived at using a Newton-directed PD-EnKF employing multi-frequency data. It is shown that the PD-EnKF provides a stable and reliable reconstruction algorithm which is also regularization-insensitive. The reference absorbed energy used in simulations is shown in figure 4(a). Figures 4(b) – 4(e) show the reconstructions for Stage-1 and Stage-2 PD-EnKFs and also a comparison with GN reconstruction. Incorporating Newton direction in the prediction step helps the filter achieve faster convergence and the evolutions of the estimates from such an experiment are reported in figure 5. Considering that, in a practical scenario, malignancies have varying absorption distributions and shape, we also show similar reconstructions for an irregular inclusion with varying absorption coefficients.

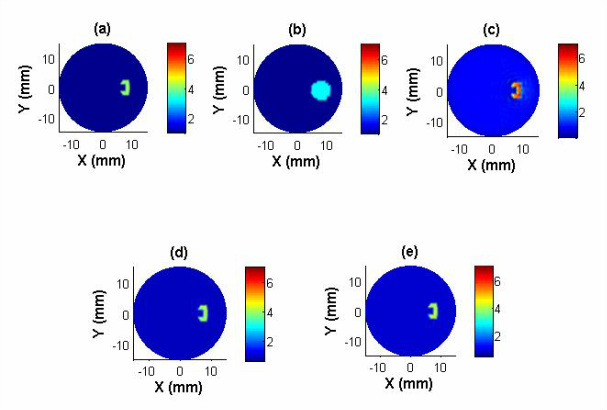
Figure 4. (a) Reference absorbed energy distribution for an inverted C-shaped inclusion, (b) location estimation of the inclusion through a shape-based PD-EnKF, (c) GN reconstruction from frequency components of boundary pressure, and reconstructions using an (d) undirected and (e) directed PD-EnKF for 60 frequencies

Figure 5. Estimation trajectories using a directed PD-EnKF for field variables in the estimated location

Direct recovery of absorption coefficient using iterated ensemble square root filter

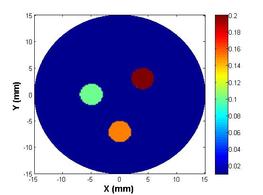
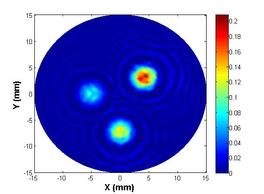
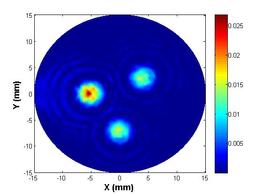
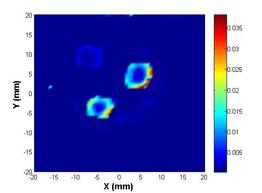
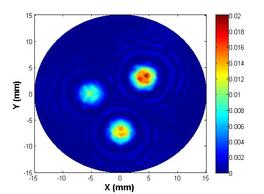
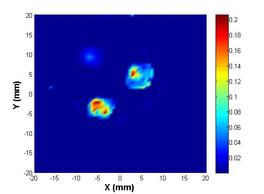
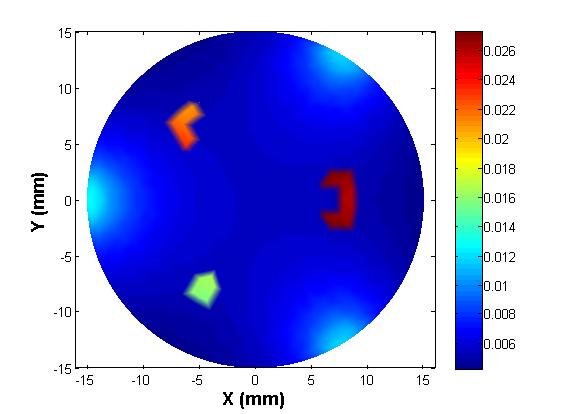
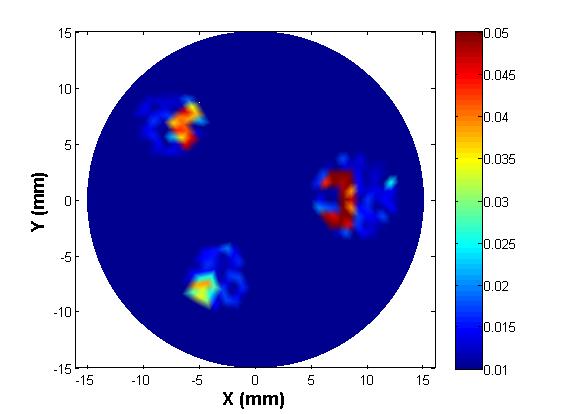
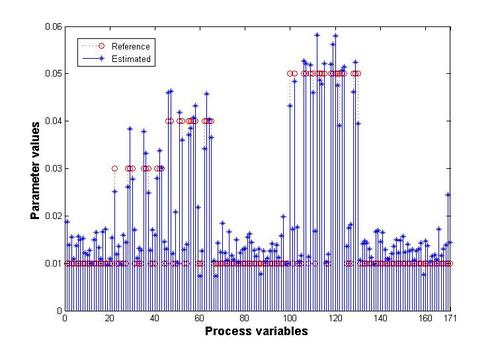
The fourth and final development is a two-stage pseudo-dynamic iterated ensemble Kalman filter (PD-IEnKF) which is used to solve for absorption coefficient directly from boundary pressure data. This is accomplished by setting up a nonlinear measurement equation relating the boundary pressure data to the optical absorption coefficient. The inclusion locations are again estimated using a shape-based Stage-1 PD-EnKF as before to help reduce the process dimension in the Stage-2 PD-IEnKF. Though the Stage-2 Newton-directed PD-EnKF elaborated earlier is able to achieve an accurate reconstruction of absorption coefficient for multiple inclusions with data from 40 frequencies, the calculation of the Jacobian matrix necessitates the solution of two forward problems in each prediction step, thereby enormously increasing the computation time. As an alternative to bringing in economy in the computation time as also to reduce the sampling variance, the Newton-direction in the prediction step is replaced with a gain-based iteration wherein we update the measurement whilst dealing with each frequency data. Such an iterative assimilation, subjected to an appropriate stopping criterion, permits an optimal data-model fitting and hence a reasonable reconstruction of absorption coefficient. The developed algorithm is computationally less expensive than the Newton-directed PD-EnKF in spite of the need to assimilate data from a larger number of frequencies. Avoidance of the intermediate absorbed energy recovery leads to a more robust and accurate algorithm. The reference distribution with three irregularly shaped optical absorption inclusions is shown below in figure 6(a); the absorbed energy map generated using three light sources (for uniform illumination and greater absorption coefficient sensitivity to measured boundary pressure) is shown in figure 6(b). The reconstructed absorption coefficient using a PD-IEnKF is given in figure 6(c). A comparison of the estimated parameters with their reference values is shown in the stem-plot of figure 7.

Figure 6. (a) Reference absorption coefficient distribution for three inhomogeneities

Figure 6. (b) Absorbed energy map generated using three sources

Figure 6. (c) Direct reconstruction of absorption coefficient from boundary pressure data at 80 frequencies through a PD-IEnKF

Figure 7. Nodal values of absorption coefficient within the regions estimated from Stage-1 EnKF

Forward solution for PAT by discontinuous Galerkin method

To efficiently predict the pressure on the object boundary, we use a DG formulation to compute the system forward model. PAT reconstruction in frequency-domain employs frequencies over a range of 40 kHz - 2 MHz. This necessitates forward solutions with very high wavenumbers. In such cases to obtain pollution free solutions, FEM calls for very dense discretizations of the physical domain which drastically increase computation times. However, tuning the DG penalty parameters can significantly reduce the pollution error and gives a better handle on generating accurate solutions for the PAT forward problem. Sharp discontinuities in the property to be reconstructed could also be accounted for.

Figure 8. (a) Absorbed energy map considered for simulations

Figure 8. (b) Pressure distribution obtained using FEM discretization

Figure 8. (c) Pressure distribution obtained using DG discretization